Some challenging calculation issues, illustrated by discovering the greatest peak in a “landscape” of many mountain peaks separated by valleys, can make the most of the Overlap Gap Property: At a high enough “altitude,” any 2 points will be either close or far apart– however absolutely nothing in-between.
David Gamarnik has actually established a brand-new tool, the Overlap Gap Property, for comprehending computational issues that appear intractable.
The idea that some computational issues in mathematics and computer technology can be tough ought to come as not a surprise. There is, in truth, a whole class of issues considered difficult to resolve algorithmically. Just listed below this class lie a little “easier” issues that are less well-understood– and might be difficult, too.
David Gamarnik, teacher of operations research study at the MIT Sloan School of Management and the Institute for Data, Systems, and Society, is focusing his attention on the latter, less-studied classification of issues, which are more pertinent to the daily world due to the fact that they include randomness– an essential function of natural systems. He and his associates have actually established a powerful tool for examining these issues called the overlap space home (or OGP). Gamarnik explained the brand-new approach in a current paper in the Proceedings of the National Academy of Sciences
P ≠ NP
Fifty years back, the most well-known issue in theoretical computer technology was developed. Labeled “P ≠ NP,” it asks if issues including large datasets exist for which a response can be confirmed fairly rapidly, however whose service– even if exercised on the fastest readily available computer systems– would take a ridiculously long period of time.
The P ≠ NP opinion is still unverified, yet most computer system researchers think that numerous familiar issues– consisting of, for example, the taking a trip salesperson issue– fall under this impossibly tough classification. The difficulty in the salesperson example is to discover the quickest path, in regards to range or time, through N various cities The job is quickly handled when N= 4, due to the fact that there are just 6 possible paths to think about. But for 30 cities, there are more than 1030 possible paths, and the numbers increase considerably from there. The most significant trouble is available in developing an algorithm that rapidly resolves the issue in all cases, for all integer worths of N. Computer researchers are positive, based upon algorithmic intricacy theory, that no such algorithm exists, therefore verifying that P ≠ NP.
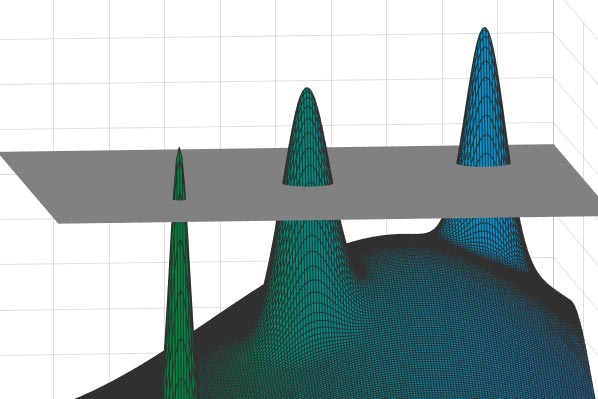
In some cases, the size of each peak will be much smaller sized than the ranges in between various peaks. Consequently, if one were to choose any 2 points on this stretching landscape– any 2 possible “solutions”– they would either be really close (if they originated from the exact same peak) or really far apart (if drawn from various peaks). In other words, there would be an obvious “gap” in these ranges– either little or big, however absolutely nothing in-between. Credit: Image thanks to the scientists.
There are numerous other examples of intractable issues like this. Suppose, for example, you have a huge table of numbers with countless rows and countless columns. Can you discover, amongst all possible mixes, the exact plan of 10 rows and 10 columns such that its 100 entries will have the greatest amount achievable? “We call them optimization tasks,” Gamarnik states, “because you’re always trying to find the biggest or best — the biggest sum of numbers, the best route through cities, and so forth.”
Computer researchers have actually long acknowledged that you can’t produce a quick algorithm that can, in all cases, effectively resolve issues like the legend of the taking a trip salesperson. “Such a thing is likely impossible for reasons that are well-understood,” Gamarnik notes. “But in real life, nature doesn’t generate problems from an adversarial perspective. It’s not trying to thwart you with the most challenging, hand-picked problem conceivable.” In truth, individuals usually come across issues under more random, less contrived situations, and those are the issues the OGP is planned to attend to.
Peaks and valleys
To comprehend what the OGP is everything about, it may initially be useful to see how the concept occurred. Since the 1970 s, physicists have actually been studying spin glasses– products with residential or commercial properties of both liquids and solids that have uncommon magnetic habits. Research into spin glasses has actually triggered a basic theory of complex systems that relates to issues in physics, mathematics, computer technology, products science, and other fields. (This work made Giorgio Parisi a 2021 Nobel Prize in Physics.)
One vexing concern physicists have actually battled with is attempting to forecast the energy states, and especially the most affordable energy setups, of various spin glass structures. The circumstance is in some cases illustrated by a “landscape” of many mountain peaks separated by valleys, where the objective is to recognize the greatest peak. In this case, the greatest peak in fact represents the most affordable energy state (though one might turn the image around and rather try to find the inmost hole). This ends up being an optimization issue comparable in type to the taking a trip salesperson’s issue, Gamarnik describes: “You’ve got this huge collection of mountains, and the only way to find the highest appears to be by climbing up each one”– a Sisyphean task equivalent to discovering a needle in a haystack.
Physicists have actually revealed that you can streamline this image, and take an action towards a service, by slicing the mountains at a specific, established elevation and overlooking whatever listed below that cutoff level. You ‘d then be entrusted a collection of peaks extending above a consistent layer of clouds, with each point on those peaks representing a possible service to the initial issue.
In a 2014 paper, Gamarnik and his coauthors saw something that had actually formerly been neglected. In some cases, they understood, the size of each peak will be much smaller sized than the ranges in between various peaks. Consequently, if one were to choose any 2 points on this stretching landscape– any 2 possible “solutions”– they would either be really close (if they originated from the exact same peak) or really far apart (if drawn from various peaks). In other words, there would be an obvious “gap” in these ranges– either little or big, however absolutely nothing in-between. A system in this state, Gamarnik and associates proposed, is defined by the OGP.
“We discovered that all known problems of a random nature that are algorithmically hard have a version of this property”– particularly, that the mountain size in the schematic design is much smaller sized than the area in between mountains, Gamarnik asserts. “This provides a more precise measure of algorithmic hardness.”
Unlocking the tricks of algorithmic intricacy
The development of the OGP can assist scientists examine the trouble of developing quick algorithms to deal with specific issues. And it has currently allowed them “to mathematically [and] carefully dismiss a big class of algorithms as possible competitors,” Gamarnik states. “We’ve learned, specifically, that stable algorithms — those whose output won’t change much if the input only changes a little — will fail at solving this type of optimization problem.” This unfavorable outcome uses not just to traditional computer systems however likewise to quantum computer systems and, particularly, to so-called “quantum approximation optimization algorithms” (QAOAs), which some private investigators had actually hoped might resolve these exact same optimization issues. Now, owing to Gamarnik and his co-authors’ findings, those hopes have actually been moderated by the acknowledgment that numerous layers of operations would be needed for QAOA-type algorithms to be successful, which might be technically tough.
“Whether that’s good news or bad news depends on your perspective,” he states. “I think it’s good news in the sense that it helps us unlock the secrets of algorithmic complexity and enhances our knowledge as to what is in the realm of possibility and what is not. It’s bad news in the sense that it tells us that these problems are hard, even if nature produces them, and even if they’re generated in a random way.” The news is not truly unexpected, he includes. “Many of us expected it all along, but we now we have a more solid basis upon which to make this claim.”
That still leaves scientists light-years far from having the ability to show the nonexistence of quick algorithms that might resolve these optimization issues in random settings. Having such an evidence would offer a conclusive response to the P ≠ NP issue. “If we could show that we can’t have an algorithm that works most of the time,” he states, “that would tell us we certainly can’t have an algorithm that works all the time.”
Predicting for how long it will take prior to the P ≠ NP issue is fixed seems an intractable issue in itself. It’s most likely there will be much more peaks to climb up, and valleys to pass through, prior to scientists get a clearer point of view on the circumstance.
Reference: “The overlap gap property: A topological barrier to optimizing over random structures” by David Gamarnik, 12 October 2021, Proceedings of the National Academy of Sciences
DOI: 10.1073/ pnas.2108492118





